Kursthemen

  • Multiplizieren mit den Fingern

    Alles einklappen Alles aufklappen

    Wohl jeder wird sich noch an seine Zeit erinnern, als man mit Hilfe der Finger Zählen gelernt hat. Doch nicht nur zum Zählen nutze man die Finger; in den ersten (und bei einigen vielleicht noch späteren) Schuljahren addierte und subtrahierte man mit den Finger. Aber kann man mit den Fingern auch multiplizieren?

  • Das Prinzip am Beispiel gezeigt

    • Das hier vorgestellte Fingermultiplizieren erlaubt nur Multiplikationen, bei denen beide Faktoren zwischen 6 und 10 liegen. Andere Produkte können nicht so bestimmt werden! Dies bedeutet aber auch, daß das 1x1 bis zur Zahl 5 beherrscht wird.

      Zunächst einmal werden die Finger beider Hände wie folgt eingeteilt:

      Und nun kann multipliziert werden. Angenommen es wird dringend das Produkt aus der Zahl 8 und 7 benötigt:

      Schritt

      Anweisung

      Beispiel

      Ergebnis
      1 Halte die Spitzen der Finger zusammen, welche die Zahlen 7 und 8 darstellen.  
      2 Zähle alle sich berührenden und darunterstehenden Finger in Zehnerschritten. 50
      3 Zähle nun die Finger einer jeden Hand über den sich berührenden und bilde das Produkt der beiden erhaltenen Zahlen 2 · 3 = 6
      4

      Addiere die Zahlen aus Schritt 2 (Zehner) und Schritt 3.

      Damit ist das Produkt bestimmt.

      7 · 8 = 56

      		 50 + 6 = 56

  • Der Hintergrund

    • Funktioniert dieses Verfahren immer? Um diese Frage zu beantworten muss die Fingerrechnung mathematisiert werden.

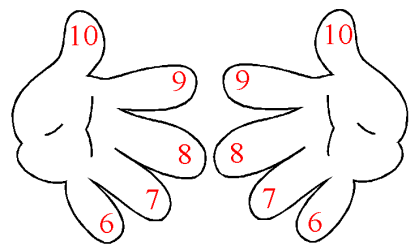
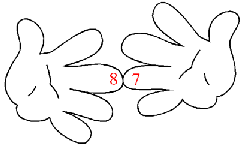
      Die Variable l soll dabei für die Nummer des Fingers stehen, welcher den Finger der anderen Hand berührt (vom kleinen Finger aus gezählt). Entsprechendes gilt dann für die Variable r. Im obigen Beispiel ist also l = 3 und r = 2.

      Berechnet werden soll also das Produkt aus 5+l und 5+r. Dazu muss man mit den Fingern

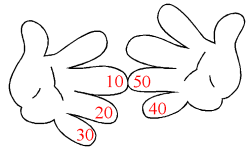
      1. sich berührende und darunter stehende Finger in Zehnerschritten zählen: 10l + 10r,
      2. die Anzahl der restlichen Fingern jeden Hand multiplizieren: (5-l)·(5-r),
      3. beides addieren, also 10l + 10r + (5-l)·(5-r).
             (5+l)·(5+r) = 10l + 10r + (5-l)·(5-r)
      25 + 5r + 5l + r·l = 10l + 10r + 25 - 5r - 5l + r·l
      25 + 5r + 5l + r·l = 25 + 5r +5l + r·l
                                                              w.z.b.w.

  • Literatur und Quellen

      • Highland und Highland: Mathematik - Ein WAS IST WAS Buch. Tessloff-Verlag, Nürnberg, 1969.